Unit and Dimensions
Unit and Dimensions
Physical Quantities
All quantities that can be measured are called physical quantities. eg. time, length, mass, force, work
done, etc. In physics we studyabout physical quantities and their inter relationships.
Measurement
Measurement is the comparison of a quantity with a standard of the same physical quantity.
Units
All physical quantities are measured w.r.t. standard magnitude of the same physical quantity and these
standards are called UNITS. e.g. second, meter, kilogram, etc.
The four basic properties of units are:
- They must be well defined.
- They should be easily available and reproducible.
- They should be invariable e.g. step as a unit of length is not invariable.
- They should be accepted to all.
Set of Fundamental Quantities
A set of physical quantities which are completely independent of each other and all other physical quantities can be expressed in terms of these physical quantities is called Set of Fundamental Quantities.
[table id=49 /]
[table id=50 /]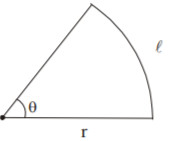
There are two supplementary units.
- Plane angle (radian) (Angle = Arc / radian, θ = l/r , l being the arc length, r is the radius and θ is the angle.
- Solid Angle (steradian)
Derived Physical Quantities
The physical quantities those can be expressed in terms of fundamental physical quantities are called
derived physical quantities. e.g. speed = distance/time.
Dimensions and Dimensional Formula
All the physical quantities of interest can be derived from the base quantities.
Dimension
The power (exponent) of base quantity that enters into the expression of a physical quantity, is called the dimension of the quantity in that base.
To make it clear, consider the physical quantity “force”.
Force = mass × acceleration
= (mass × length)/(time × time)
= mass × length × (Time)-2
So the dimensions of force are 1 in mass, 1 in length and –2 in time. Thus
[Force] = M L T-2
Similarly energy has dimensional formula given by
[Energy ] = M L2 T-2
i.e. energy has dimensions, 1 in mass, 2 in length and -2 in time.
Such an expression for a physical quantity in terms of base quantities is called dimensional formula.
Dimensional Equation
Whenever the dimension of a physical quantity is equated with its dimensional formula, we get a dimensional
equation.
Principle of Homogeneity
According to this principle,we can multiply physical quantities with same or different dimensional formula
at our convenience, however no such rule applies to addition and subtraction, where only like
physical quantities can only be added or subtracted. e.g. If P + Q ⇒ P & Q both represent same
physical quantity.
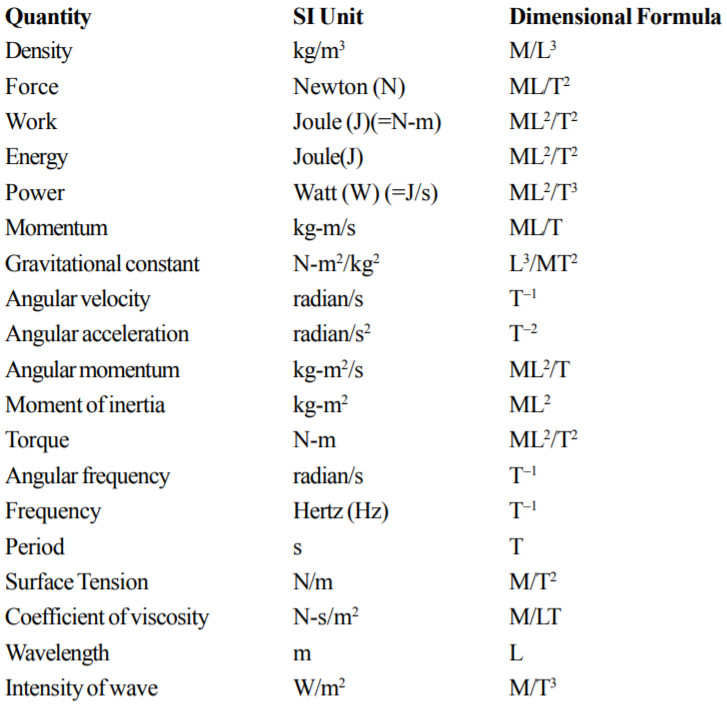
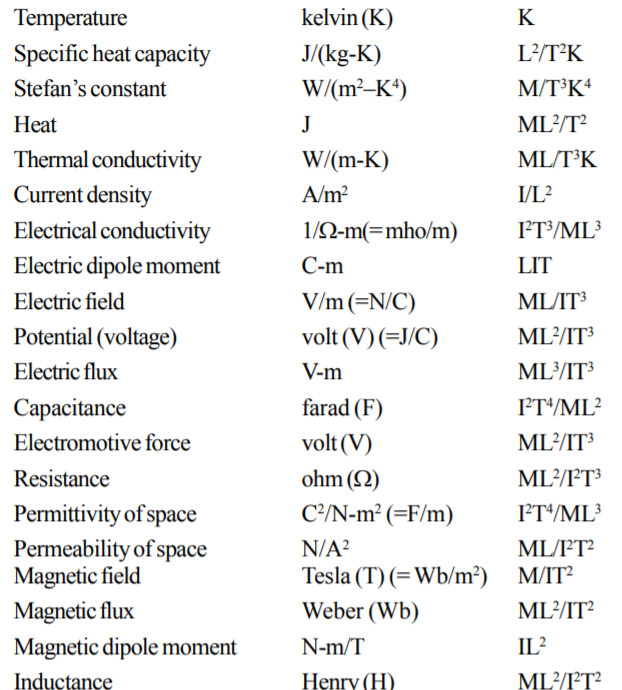
Units and Dimensions of some physical Quantities
LIMITATIONS OF DIMENSIONAL ANALYSIS
(i) Dimension does not depend on the magnitude. Due to this reason the equation x = ut + at2 is also dimension ally correct. Thus, a dimension ally correct equation need not be actually correct.
(ii) The numerical constants having no dimensions con not be deduced by the method of dimensions.
(iii) This method is applicable only if relation is of product type. It fails in the case of exponential and
trigonometric relations.
SI Prefixes : The magnitudes of physical quantities vary over a wide range. The mass of an electron is
9.1 × 10-31 kg and that of our earth is about 6 × 10-24 kg. Standard prefixes for certain power of 10.
Table shows these prefixes :
[table id=53 /]
