Square Root RRB
Square Root
The square root of a number is that number the product of which itself gives the given number, ie, the square root of 400 is 20, the square root of 625 is 25.
The radical sign:
The expression √16 is read as root sixteen. Some times also square root of 16, or radical of sixteen.
How to find square root of an integer?
i) By prime factorization method:
When a given number is a perfect square we resolve it into prime factors and take the product of prime factors choosing one out of every two.
Example 1: Find the square root of 4356.
Ans:
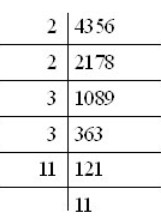
4356 = 2×2×3×3×11×11
Hence √4356 = 2×3×11 = 66
Thus from the above example it is clear that in order to find the complete square root of a given number every prime factor of that number should be repeated twice. Thus, we can make a number which is not a perfect square, a perfect square by multiplying or dividing the number by those factors of it which are not contained in pairs.
Example 2: The square root of (7 + 35) (7 – 35) is
Ans: ![]()
Example 3: The square root of 64009 is
Ans:

Example 4: Find the square root of 484 by prime factorization method.
Ans: Resolving 484 as the product of primes, we get,
√484 = √(2 × 2 × 11 × 11) = 2 × 11
Therefore, √484 = 22.
Example 5: Find out the square root of 1764.
The square root of 1764 by prime factorization, we get
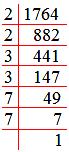
1764 = 2 x 2 x 3 x 3 x 7 x 7.
√1764 = √(2 x 2 x 3 x 3 x 7 x 7)
= 2 x 3 x 7
Therefore, √1764 = 42.
Cube Root:
The cube root of a number is that number the cube of which itself gives the given number i.e. the cube root of 125 is 5. The cube root of a number is denoted by the symbol ![]() . The expression
. The expression ![]() is read as cube root of 64.which is 4.
is read as cube root of 64.which is 4.
To find the cube root of an integer:
By prime factorization method:
When a given number is a perfect cube, we resolve it into prime factors and take the product of prime factors, choosing one out of every three.
Example 1: Find the cube root of 74088.
Ans:
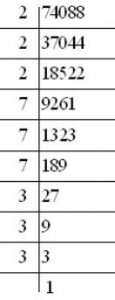
Hence 74088 = 2×2×2×7×7×7×3×3×3 =2³×3³×7³
and the cube root of 74088 = 2×3×7 = 42
Example 2: The cube root of .000216 is,
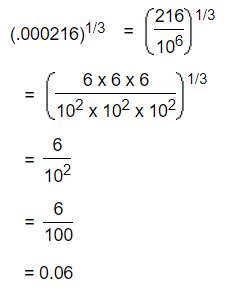
Example 3: The cube root of .000216 is:
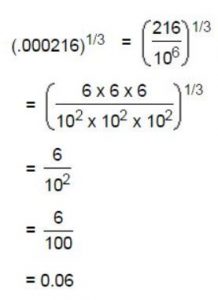
Example 4: Find the cube root of 19683.
Ans: In 19683, 19 lies between 2³ and 3³, so left digit is 2 and 683 ends with 3, so right digit is 7. Thus 27 is a cube root of 19683.
Example 5: Evaluate the cube root: ∛343
Ans: By prime factorization, we have
343 = 7 × 7 × 7
= (7 × 7 × 7).
Therefore, ∛343 = 7.
