Average, Weight, Height, Age and Marks-RRB
Average:
An average is a middle or typical number of a list of numbers.
A number expressing the central or typical value in a set of data, in particular the mode, median, or (most commonly) the mean, which is calculated by dividing the sum of the values in the set by their number.
Average = (Sum of observations)/(Number of observations)
Average Speed:
Suppose a man covers a certain distance at x kmph and an equal distance at y kmph.
Then, the average speed during the whole journey = 2xy/(x+y)
Arithmetic Mean:
The most common type of average is the arithmetic mean. If n numbers are given, each number denoted by ai (where i = 1,2, …, n), the arithmetic mean is the sum of the as divided by n or
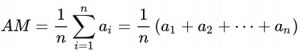
The arithmetic mean, often simply called the mean, of two numbers, such as 2 and 8, is obtained by A = (2 + 8)/2 = 5
Geometric Mean:
The geometric mean of n positive numbers is obtained by multiplying them all together and then taking the nth root. In algebraic terms, the geometric mean of a1, a2, …, an is defined as
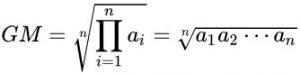
Example: Geometric mean of 2 and 8 is √2.8 = 4
Harmonic mean:
Harmonic mean for a non-empty collection of numbers a1, a2, …, an, all different from 0, is defined as the reciprocal of the arithmetic mean of the reciprocals of the ai‘s:
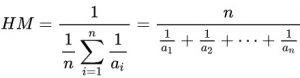
Example
If the speed for going from point A to B was 60 km/h, and the speed for returning from B to A was 40 km/h, then the harmonic mean speed is given by
2/(1/60 + 1/40) = 2×120/(2+3) =2 × 24 = 48
Inequality concerning AM, GM, and HM:
A well known inequality concerning arithmetic, geometric, and harmonic means for any set of positive numbers is
It is easy to remember noting that the alphabetical order of the letters A, G, and H is preserved in the inequality.
Thus for the above harmonic mean example: AM = 50, GM ≈ 49, and HM = 48 km
Example on Weight
Example-1
The average weight of 8 persons increases by 2.5 kg when a new person comes in place of one of them weighing 65 kg. What might be the weight of the new person ?
Solution
Total weight increased = (8 x 2.5) kg = 20 kg.
Weight of new person = (65 + 20) kg = 85 kg.
Example-2
The average weight of a class of 24 students is 35 kg. If the weight of the teacher be included, the average rises by 400 g. The weight of the teacher is :
Answer
Weight of the teacher = (35.4 x 25 – 35 x 24) kg = 45 kg.
Example-3
In Arun’s opinion, his weight is greater than 65 kg but leas than 72 kg. His brother does not agree with Arun and he thinks that Arun’s weight is greater than 60 kg but less than 70 kg. His mother’s view is that his weight cannot be greater than 68 kg. If all of them are correct in their estimation, what is the average of different probable weights of Arun ?
Solution
Let Arun’s weight be X kg.
According to Arun, 65 < X < 72.
According to Arun’s brother, 60 < X < 70.
According to Arun’s mother, X < 68.
The values satisfying all the above conditions are 66 and 67.
Required average = (66 + 67) / 2 = 66.5 kg
Examples of Height
Example-1
A student was asked to find the arithmetic mean of the heights of kids playing of heights 5′, 4′, 6′, 5′, 5′, 5′, 4′, 5′, 5′, 6′, 4′ feets respectively and one of x feet. He found the mean of height to be 5′. What should be the height of kid in place of x ?
Solution
we have (5’+ 4’+ 6′ + 5’+ 5’+ 5’+4’+ 5’+ 5’+ 6’+ 4′ + x)/12
(54+x) / 12 = 5.
or 54 + x = 60
Hence x =6.
Examples on marks
Example-1
David obtained 76, 65, 82, 67 and 85 marks (out of 100) in English, Mathematics,Physics, Chemistry and Biology What are his average marks ?
Solution
Average = (76 + 65 + 82 + 67 + 85 )/ 5 = 375/5 = 75
Example-2
A team of 8 persons joins in a shooting competition. The best marksman scored 85 points. If he had scored 92 points, the average score for the team would have been 84. The number of points, the team scored was :
Solution
Let the total score be x.
(x + 92 – 85) / 8 = 84.
So, x + 7 = 672 => x = 665.
Example-3
In an examination, a pupil’s average marks were 63 per paper. If he had obtained 20 more marks for his Geography paper and 2 more marks for his History paper, his average per paper would have been 65. How many papers were there in the examination ?
Solution
Let the number of papers be x. Then, 63x + 20 + 2 = 65x or 2x = 22 or x = 11
Example-4
A pupil’s marks were wrongly entered as 83 instead of 63. Due to that the average marks for the class got increased by half. The number of pupils in the class is :
Solution:
Let there be x pupils in the class.
Total increase in marks = (x ×1/2) = x/2.
x/2 = (83 – 63) => x/2 = 20 => x = 40.
Examples on Age
Example-1
The average age of 36 students in a group is 14 years. When teacher’s age is included to it, the average increases by one. What is the teacher’s age in years ?
Solution
Age of the teacher = (37 × 15 – 36 × 14) years = 51 years
Example-2
The average age of a husband and his wife was 23 years at the time of their marriage. After five years they have a one-year old child. The average age of the family now is :
Solution
Sum of the present ages of husband, wife and child = (23 * 2 + 5 * 2) + 1 = 57 years.
Required average = (57/3) = 19 years.
Example-3
The average age of students of a class is 15.8 years. The average age of boys in the class is 16.4 years and that of the girls is 15.4 years, The ratio of the number of boys to the number of girls in the class is :
Solution
Let the ratio be k : 1. Then,
k × 16.4 + 1 × 15.4 = (k + 1) × 15.8
⇔ (16.4 – 15.8) k = (15.8 – 15.4) ⇔ k = 0.4/0.6 = 2/3.
Required ratio = 2/3 : 1 = 2 : 3.
Example-4
The average age of 8 men is increased by years when two of them whose ages are 21 years and 23 years are replaced by two new men. The average age of the two new men is :
Solution
Total age increased = (8 × 2) years = 16 years.
Sum of ages of two new men = (21 + 23 + 16) years = 60 years
Average age of two new men = (60/2) years = 30 years.
Example-5
After replacing an old member by a new member, it was found that the average age of five members of a club is the same as it was 3 years ago. What is the difference between the ages of the replaced and the new member ?
Solution
i) Let the ages of the five members at present be a, b, c, d & e years.
And the age of the new member be f years.
ii) So the new average of five members’ age = (a + b + c + d + f)/5 ——- (1)
iii) Their corresponding ages 3 years ago = (a-3), (b-3), (c-3), (d-3) & (e-3) years
So their average age 3 years ago = (a + b + c + d + e – 15)/5 = x —– (2)
==> a + b + c + d + e = 5x + 15
==> a + b + c + d = 5x + 15 – e —— (3)
iv) Substituting this value of a + b + c + d = 5x + 15 – e in (1) above,
The new average is: (5x + 15 – e + f)/5
Equating this to the average age of x years, 3 yrs, ago as in (2) above,
(5x + 15 – e + f)/5 = x
==> (5x + 15 – e + f) = 5x
Solving e – f = 15 years.
Thus the difference of ages between replaced and new member = 15 years.
Example-6
10 years ago, the average age of a family of 4 members was 24 years. Two children having been born (with age difference of 2 years), the present average age of the family is the same. The present age of the youngest child is :
Solution
Total age of 4 members, 10 years ago = (24 x 4) years = 96 years.
Total age of 4 members now = [96 + (10 x 4)] years = 136 years.
Total age of 6 members now = (24 x 6) years = 144 years.
Sum of the ages of 2 children = (144 – 136) years = 8 years.
Let the age of the younger child be x years.
Then, age of the elder child = (x+2) years.
So, x+(x+2) =8 <=> x=3
Age of younger child = 3 years.

