Simple Ratio and Compound Ratio-RRB
Simple Ratio
The ratio which is simplified to its lowest numerical relationship by removing common factors is called simple ratio. A simple whole number ratio is when both the numerator and denominator are natural numbers of any size, but are co-prime. To find an equal ratio, you can either multiply or divide each term in the ratio by the same number (but not zero). For example, if we divide both terms in the ratio 3:6 by the number three, then we get the equal ratio, 1:2. Do you see that these ratios both represent the same comparison?
Example:
- Simple ratio of 10 : 15 = 2 : 3
- simple ratio of 20 : 25 = 4: 5
- Simple ratio of 39 : 130= 3 : 10
Say for instance, you are in a classroom. In the classroom, there are 5 boys and 9 girls.
The ratio of boys to girls is: 5/9
Ratio of girls to number of students in the classroom: 9/14
Compound Ratio
Compound ratio is the product of two or more ratios. When two or more ratios are multiplies term wise; the ratio thus obtained is called compound ratio. For example: The compounded ratio of the two ratios a : b and c : d is the ratio ac : bd, and that of a : b, c : d and e : f is the ratio ace : bdf. For ratios m : n and p : q; the compound ratio is (m × p) : (n × q).
Example 1:
a : b and c : d Re the two ratio then ab : cd is the compounded ratio of a : b and c : d
Example 2:
If the compound ratio of 7 : 5 and 8 : x is 84 : 60, find x
Solution:
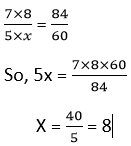
Example 3:
A bag contains 50 P, 25 P and 10 P coins in the ratio 5: 9: 4, amounting to Rs. 206. Find the number of coins of each type respectively.
Solution:
Let ratio be x.
Hence no. of coins be 5x, 9x, 4x respectively
Now given total amount = Rs.206
=> (.50)(5x) + (.25)(9x) + (.10)(4x) = 206
we get x = 40
=> No. of 50p coins = 200
=> No. of 25p coins = 360
=> No. of 10p coins = 160
Example 4:
Salaries of Ravi and Sumit are in the ratio 2:3. If the salary of each is increased by Rs. 4000, the new ratio becomes 40:57. What is Sumit’s salary?
Solution:
Let the original salaries of Ravi and Sumit be Rs. 2x and Rs. 3x respectively.
Then,
(2x+4000) / (3x+4000) = 40 / 57
⇒ 57 × (2x + 4000) = 40 × (3x+4000)
⇒ 6x = 68,000
⇒ 3x = 34,000
Sumit’s present salary = (3x + 4000) = Rs.(34000 + 4000) = Rs. 38,000
Example 5:
Seats for Mathematics, Physics and Biology in a school are in the ratio 5:7:8. There is a proposal to increase these seats by 40%, 50% and 75% respectively. What will be the ratio of increased seats ?
Solution:
Originally, let the number of seats for Mathematics, Physics and Biology be 5x, 7x and 8x respectively.
Number of increased seats are (140% of 5x), (150% of 7x) and (175% of 8x).
⇒ [(140/100) × 5x],[(150/100) × 7x] and [(175/100) × 8x]
⇒ 7x, 21x/2 and 14x.
⇒ The required ratio =7x : 21x/2 : 14x
⇒ 14x : 21x : 28x
⇒ 2 : 3 : 4
Duplicate ratio: Duplicate ratio is the ratio of two equal ratios.
For example:
The duplicate ratio of the ratio x : y is the ratio x² : y²
In other words,
The duplicate ratio of the ratio m : n = Compound ratio of m : n and m : n
= (m × m) : (n × n)
= m² : n²
Therefore, the duplicate ratio of 4 : 7 = 4² : 7² = 16 : 49
Triplicate ratio: The triplicate ratio is the compound ratio of three equal ratios.
The triplicate ratio of the ratio a : b is the ratio a³ : b³ .
In other words,
The triplicate ratio of the ratio m : n = Compound ratio of m : n, m : n and m : n
= (m × m × m) : (n × n × n)
= m³ : n³
Therefore, the triplicate ratio of 4 : 7 = 4³ : 7³ = 64 : 343.
Sub duplicate ratio: The sub duplicate ratio m : n is the ratio √m : √n. So, the sub duplicate ratio of the ratio m² : n² is the ratio m : n.
For example: The sub duplicate ratio of 25 : 81 = √25 : √81 = 5 : 9.
Sub triplicate ratio: The sub triplicate ratio m : n is the ratio √m : √n. So, the sub triplicate ratio of the ratio ³√
: ³√ is the ratio m : n.
For example: The sub triplicate ratio of 125 : 729 = ³√ : ³√= 5 : 9
Reciprocal ratio: The reciprocal ratio of the ratio m : n (m ≠ 0, n ≠ 0) is the ratio 1/m : 1/n
For any ratio x : y, where x, y ≠ 0, its reciprocal ratio = 1/x : 1/y = y : x
Similarly, we can say if the antecedent and consequent of a ratio be interchanged, the changed ratio is called the inverse ratio of the previous ratio.
For example: Reciprocal ratio of 7 : 13 = 1/7 : 1/13 = 13:7 is the inverse ratio of 7:13 .
Ratio of equalities: For a ratio, if the antecedent and consequent are equal, the ratio is called ratio of equality.
For example: 5 : 5 is the ratio of equalities.
Ratio of inequalities: For a ratio, if the antecedent and consequent are unequal, the ratio is called ratio of inequality.
For example: 5 : 7 is the ratio of inequalities.
Ratio of lesser inequalities: For a ratio, if antecedent is less than the consequent, the ratio is called the ratio of lesser inequality.
For example: 7 : 9 is a ratio of lesser inequalities.
Ratio of greater inequalities: For a ratio, if antecedent is greater than the consequent, the ratio is called the ratio of greater inequality.
For example: 13 : 10 is a ratio of greater inequalities.
Note: (i) If the ratio x : y, if x = y, we get ratio of equality. If x ≠ y, we get ratio of inequality, x > y gives ratio of greater inequality.
(ii) y : x and x : y are mutually inverse ratio to each other.
