Simple Interest-RRB

Simple Interest

In simple interest we will learn and identify about the terms like Principal, Time, Rate, Amount, etc.

Suppose Ron has deposited $100 in a bank. Ron goes to the bank to find out about his deposited money. The manager of the bank informs Ron that $100 deposited in the bank one year before has now become $110. Ron enquires how did $100 become $110 after one year?

The manager told that when someone deposits money in a bank, we pay some extra money on the deposited amount.

For example, suppose the bank has given a loan of $6000 to Jack to purchase a tractor. After three years Jack returns back the loan along with 10% interest charged by the bank.

Here, the money borrowed (loan is the principal and the extra money to be paid is called the interest.

The interest is only a fair payment for using another person’s money.

Principal (P):

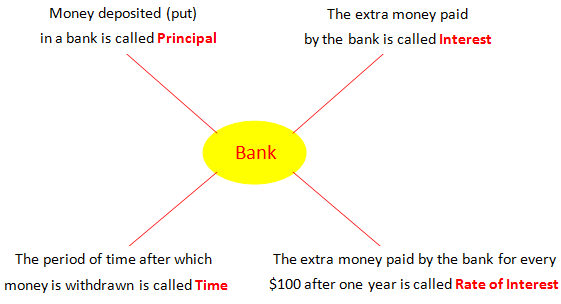
The money you deposit or put in the bank is called the PRINCIPAL.

Interest (I):

The extra money you get from the bank after depositing is called the Interest.

Amount(A):

The total money means the Principal and Interest you get after a fix time is called the Amount.

Notes:

P is the money deposited or borrowed called the Principal.

T is the Time or number of years for which the money is deposited or borrowed.

The interest is calculated at a Rate per cent decided by the bank every year. This is R % p.a. (per annum or per year)

PRINCIPAL (P) + INTEREST (I) = AMOUNT (A)

OR
P + I = A

There are two types of interests.

1. Simple Interest (S.I.).

2. Compound Interest (C.I.).

The Simple Interest (SI) remains the same every year.

Question 1:

A certain sum of money amounts to Rs.2000 in 2 years and to Rs.2500 in 3 years. Find the sum and rate of interest.

Solution:

Let P be the amount invested.
You know that the amount becomes 2000 in 2 years and 2500 in 3 years. You can see that the amount increases by Rs. 500 between 2nd and 3rd years.

Therefore, you can easily say that the simple interest for 1 year = 2500 – 2000 = 500
So, simple interest for 2 years = 500 x 2 = 1000
From the question, you know that the amount A after 2 years = 2000

Now using the formula A = P + SI,
you can write P = A – SI = 2000 – 1000 = 1000

Now, you know P = Rs.1000, N = 2 years and Simple interest SI = Rs.1000.
If you substitute above values in the formula SI = P*N*R / 100, you will get R as shown below:
R = (100 x 1000) / (1000 x 2)
R = 50%
Therefore, the sum invested P = 1000 and rate of interest R = 50%.

Question 2:

A man borrowed Rs 15000/- at the rate of 24% SI and to clear the debt after 6 years, much he has to return:

Using the Basic Formula:
Simple Interest (SI) = (P x R x T)/100
P – Principal amount, T- Number of years, R – Rate of Interest
Given P = 15000, T = 6 Years, R = 24%
Simple Interest (S.I.) = (15000X24X6)/100= Rs 21600
Therefore, total interest = 21600
Total repayment = S.I + Principal amount = 21600 + 15000 = Rs 36600

Question 3:

A man borrowed Rs.12000 at the rate of 10% SI, and lent the same sum to another person at the rate of 15% what will be the gain after 5 years?

Using the Basic Formula:
Simple Interest (S.I.) = (P x R x T)/100
P – Principal amount, T- Number of years, R – Rate of Interest

The man borrowed at 10% and he lent the same sum to another person at 15%
Therefore, his gain is actually equal to the different in the interest rate (per year)
= 15 – 10 =5% for 1 year
Thus, to calculate his gain, we use this difference as the rate of interest.
Given T = 5 years and P = Rs. 12000
Amount Gained = (12000x5x5)/100 = Rs 3000
Therefore, his gain = Rs 3000/-

Question 4:

A certain sum of money amounts to Rs. 1008 in 2 years and to Rs. 1164 in 3¹⁄₂ years. find the sum and the rate of interest?

S.I. for 1¹⁄₂years = Rs. (1164-1008) =156

S.I. for 2 years = Rs. (156 x ²⁄₃ x 2) = Rs. 208

Principal = Rs. (1008 – 208) = Rs. 800

Now, P = 800, T = 2, and S.I. = 208

Rate = (^100×208⁄_800×2)% = 13%

Question 5:

At what rate percent per annum will a sum of money double in 8 years.

Let principal = P, Then, S.I.= P and Time = 8 years

We know that S.I. = PTR/100

Rate= [(100 x P)/ (P x 8)]% = 12.5% per annum.

Question 6:

What annual installment will discharge a debt of Rs 1092 due in 3 years at 12% simple interest?

Let each instalment be Rs.x .

1st year =  [x + (x * 12 * 2)/100]

2nd year = [ x + (x *12 * 1)/100]

3rd year = x

Then, [x + (x * 12 * 2)/100] + [ x + (x *12 * 1)/100] + x =1092

3x + ( 24x/100 ) + ( 12x/100 )  = 1092

336x =109200

Therefore, x = 325

Each installment = Rs. 325

Question 7:

A sum was put at simple interest at a certain rate for 3 years. Had it been put at 2% higher rate, it would have fetched Rs 360 more. Find the sum.

Let sum = P and original rate = R. Then

[(P * (R+2) * 3)/100] – [ (P * R * 3)/100] = 360

3P*(R+2) – 3PR = 36000

3PR + 6P – 3PR = 36000

6P = 36000

P = 6000