Compound Interest-RRB
Compound interest
Under this topic, we will be studying about compound interest. Compound interest is defined as the interest calculated on both the amount borrowed (i.e., principal amount) and any previous interest. It is also known as interest on interest. Compound interest is standard in finance and economics.
Below are given some formula used in compound interest:
Let P be the principal amount R% be the rate of interest and T be the time given to repay the amount. Then, amount to be repaid, i.e., A is given by:
I. When the interest is compounded yearly:
A =P(1 + R/100)T
II. When the interest is compounded half yearly:
A = P(1 + R/200)2T
III. When the interest is compounded quarterly:
A = P(1 + R/400)4T
IV. When the time is in fraction of a year, say 21/5
A = P(1 + R/100)2 (1 + R/500)
V. If the rate of interest in 1st year, 2nd year, 3rd year,…, nth year are R1%, R2%, R3%,…, Rn% respectively. Then,
A = P(1+R1/100)(1+R2/100)(1+R3/100)...(1+Rn/100)
The above given formulae are sufficient to find the amount to be repaid when the interest is compound interest. We know that:
A = P + I
where, A = amount to be repaid
P = Principal amount
I = interest
So, interest = amount – principal amount
Compounding frequency:
The compounding frequency is the number of times the accumulated interest is paid in a year on a regular basis. The frequency could be yearly, half-yearly, quarterly, weekly, or even daily until the loan is completely paid along with the interest.
Look at the below given example to get a better view to calculate compound interest:
Example
A rate of 12.5% is charged on a principal sum of $12,000. The time given to repay the amount is 2 years. If the interest is compounded annually, then calculate the amount to be repaid and interest charged in two years.
Solution:
Interest rate = 12.5%
Principal amount = $12,000
Time = 2 years
Total interest = ?
Amount = ?
We know that A = P(1+R/100)T
So, A = 12,000(1+12.5100)2
= $15,187.5
Interest = amount – principal
= $15,187.5 – $12,000
= $3,187.5
Question 1:
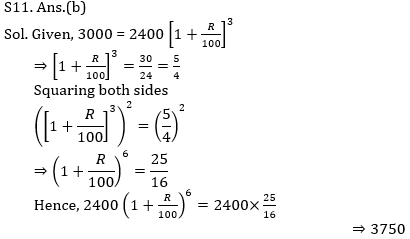
Question 2:
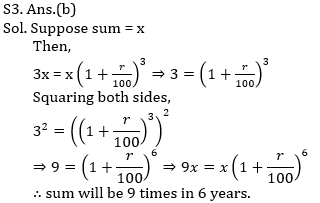
Question 3:
Find the compound interest on Rs. 20,000 in 2 years at 4 % per annum, the interest being compounded half-yearly.
Solution:
Principal = Rs. 20000, Rate = 2 % per half-year, Time = 2 years = 4 half- years
Question 4:
The compound interest on a certain sum for two years at 20% per annum is Rs 770. If the same sum is lent for 3 years at simple interest for 1% per month, find the interest obtained on the sum.
A.Rs 525
B. Rs 550
C. Rs 660
D. Rs 630
E. None of these
Solution
Option – D

