Volume of Cube, Cuboid, Cylinder, Cone Tetrahedron, Pyramid-RRB
Volume Of Cube
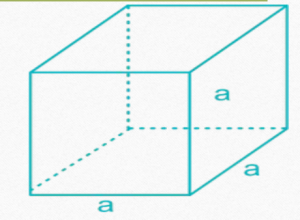
In the following formulae, a = side of a cube
• Volume of cube = a³
• Total surface area of cube = 6a²
• Length of Leading Diagonal of Cube = a√3
Volume Of Cuboid
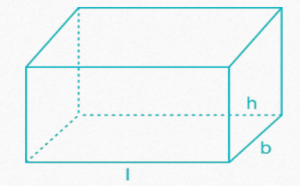
In the following formulae, l = length, b = breadth and h = height
• Total surface area of cuboid = 2 (lb + bh + lh)
• Length of diagonal of cuboid= √(l²+b²+h²)
• Volume of cuboid = l × b × h
Volume Of Cone
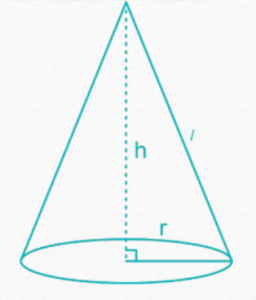
In the following formulae, r = radius of base, l = slant height of cone and h = height
of the cone (perpendicular to base)
• Slant height of a cone = l =√(h²+r²)
• Curved surface area of a cone = C = π × r × l
• Total surface area of a cone = π × r × (r + l)
• Volume of right circular cone =1/3 πr²h
Volume Of Cylinder
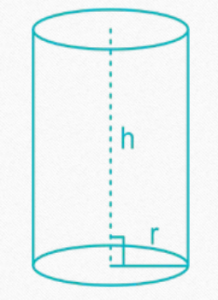
In the following formulae, r = radius of base, h = height of cylinder
• Curved surface area of a cylinder = 2πrh
• Total surface area of a cylinder = 2πr(r + h)
• Volume of a cylinder = πr²h
Volume Of Hollow Cylinder
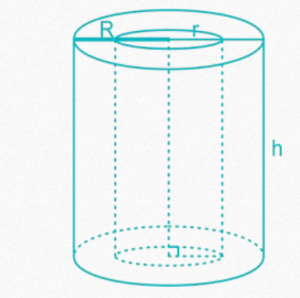
Hollow cylinder made by cutting a smaller cylinder of same height and orientation
out of a bigger cylinder.
Volume of hollow cylinder = πh(R²– r²)
(Where, R = radius of cylinder,
r = radius of cavity, h = height of cylinder)
Volume Of Pyramid
• Pyramid consists of a polygonal base and triangles at its sides. These triangles are called faces.
• The base could be of any shape, whereas the faces are generally isosceles triangles.
• All these triangular faces meet in a single point called the apex.
• Total surface area of pyramid= base area + (number of sides × ½ × slant height × base length)
• Volume of pyramid = (1/3) × base area × height
Volume Of Tetrahedron
The tetrahedron is made up of four equilateral triangles, all its edges are the same. Remember, an equilateral triangle is a triangle with three congruent, or equal, sides. So you actually only have one value, and the same measurement for each and every edge of the tetrahedron. And, this is the only measurement you need to find your volume and surface area.
To find the volume of a tetrahedron, you’ll use this formula:
 |
The a stands for the length of one of the edges of the tetrahedron.
All you need to find the volume is the value for a. Once you have this number, then you can go ahead and plug it in and find your answer.
For example, if the tetrahedron has an edge length of 3 inches, then your volume would be calculated like this:
 |
We multiply all of this out and get the volume of this tetrahedron with an edge of 3 inches is 3.18 cubic inche
Example – 1
Find the volume if the length of one side is 2 cm
Solution
Vcube = 23
Vcube = 2 × 2 × 2
Vcube = 8 cm3
Example – 2
Find the volume if the length of one side is 3 cm
Solution
Vcube = 33
Vcube = 3 × 3 × 3
Vcube = 27 cm3
Example – 3
Find the volume if the length of one side is 3/2 cm
Solution
Vcube = (3/2)3
Vcube = 3/2 × 3/2 × 3/2
Vcube = (3 × 3 × 3)/(2 × 2 × 2) Vcube = 27/8 Vcube = 3.375 cm3
Example – 4
Find the volume of a cereal packet whose length = 8, width = 20 and height = 30
Solution
The volume of this cereal packet is:
volume = l × w × h
8 × 20 × 30 = 4800 cm3
Example – 5
Find the volume of a cuboid of dimensions 16 cm x 10 m x 6 cm.
Solution
Volume of cuboid = l x b x h = 16 x 10 x 6 = 960 cu cm
Example – 6
Find the volume of a cuboid of dimensions 18 cm x 30 mm x 15 cm.
Solution
l = 18 cm, b = 30 mm = 3 cm (10 mm =1 cm, 30/10 = 3 cm), h = 15 cm
Volume of cuboid = l b
h = 18
3
15 = 810 cu cm
Example – 7
Find the volume of a cuboid of dimensions 21 mm 2 cm
12 mm in cu. cm.
Solution
10 mm = 1 cm
Therefore, 21 mm = 21/10 cm = 2.1 cm, 12 mm = 12/10 = 1.2 cm
Length = 2.1 cm, breadth = 2 cm, height = 1.2 cm
Volume of cuboid = l b
h = 2.1
2
1.2 = 5.04 cu cm
Example – 8
Find the number of cubical boxes of cubical side 5 cm, which can be accommodated in carton of dimensions 25 cm x 10 cm x 15 cm.
Solution
Volume of cubical box = side x side x side = 5 5
5 = 125 cu cm
Volume of carton = 25 10
15 = 3750 cu cm
No. of boxes = Volume of carton/Volume of each box = 3750/125 = 30
Example – 9
What is the volume of a cone with a circular base with a radius of 5 cm and a height of 10 cm, as shown below?
Solution
Volume = πr2h ⁄ 3
Volume = π × 52 × 10 ⁄ 3
Volume = π × 5 × 5 × 10 ÷ 3
Volume = π × 250 ÷ 3
Volume = 3.14 × 250 ÷ 3
Volume = 262 cm3
Example – 10
A tool is made up of a cone on top of a cylinder (see figure below). The cylinder has a height h of 15 cm and a radius of 5 cm. The volume of the cone is 100 Pi cm 2. O is the vertex of the cone, AB is the diameter of the base of the cone and C its center. Points O, A, B and C are in the same plane.
1 – Approximate angle AOB.
2 – Calculate the area of the lateral surface of the tool.
Solution
- We first use the formula of the volume of the cone to find its height H:(1 / 3)
Pi
5 2
H = 100 Pi
- Solve for H : H = 12 cm
- Since OC is orthogonal to the base, triangle AOC is a right triangle. tan(angle AOC) is given by:tan(angle AOC) = r / H = 5 / 12 angle AOC = arctan(5 / 12)
- Because of the symmetry of the tool, the size of angle AOB is twice the size of angle AOC, hencesize of angle AOB = 2
arctan (5 / 12) = 45.2 degrees (approximated to 1 decimal place).
- The area lateral surface of the cone and that of the cylinder are added to obtain the total area A of the surface.A = Pi
r
sqrt [ H 2 + r 2 ] + 2
Pi
r
h= Pi
5
sqrt [ 12 2 + 5 2 ] + 2
Pi
5
15= 675.4 cm 2
Example – 11
Calculate the volume of a cylinder where:
a) the area of the base is 30 cm 2 and the height is 6 cm.
b) the radius of the base is 14 cm and the height is 10 cm.
Solution
a)
b)
Example – 12
Calculate the radius of base of a cylindrical container of volume 440 cm3. Height of the cylindrical container is 35 cm. (Take = 22/7)
Solution
Volume of a cylinder = (area of base) × height of cylinder
Area of base = (Volume of cylinder)/ (height of cylinder) = 440/35cm2
⇒ 22/7× r2 = 440/35
⇒ r2 = 4
⇒ r = 2 cm
Example – 13
Calculate the volume of a cylinder having height 20 cm and base radius of 14 cm. (Take = 22/7)
Solution
Volume of a cylinder = r2 h
⇒ 22/7×14×14×20 = 12320 cm3
Example – 14
Find the volume of a rectangular-based pyramid whose base is 8 cm by 6 cm and height is 5 cm.
Solution
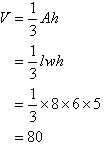
Example – 15
Find the volume of the following triangular pyramid, rounding your answer to two decimal places.
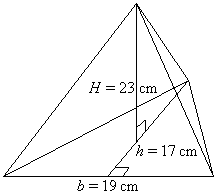

Example – 16
Find the volume of a pyramid with a rectangular base measuring 6 cm by 4 cm and height 10 cm.
Solution
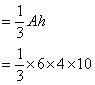
= 80 cm3
Example – 17
The following figure is a right pyramid with an isosceles triangle base. Find the volume of the pyramid if the height is 20 cm.

Solution:
First, we have to calculate the area of the base.
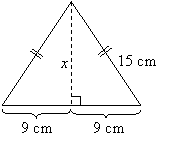
To do that, we would need to get the height of the isosceles triangle that forms the base.
Using Pythagorean theorem,
![]()
Area of triangle
= ![]()
= 108 cm2
Volume of pyramid
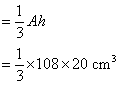
= 720 cm3
Example – 18
A trapezoid ABCD with AD parallel to BC has angle D equal to 40 degrees, the length of DC is equal to 2 meters, the length of BC is equal to 5 meters and the area of the trapezoid is equal to 20 m 2. Calculate the length of AD.
Solution
Use the sine definition in a right triangle to find the height h of the trapezoid.
sin D = h / CD
Solve the above for h.
h = CD sin D = 2
sin 40
Use the formula of the area to obtain the following equation.
area of trapezoid ABCD = 0.5 h
(BC + AD)
The above equation has only one unknown: AD. Substitute all the known quantities to obtain
20 = 0.5 2
sin 40
(5 + AD)
Solve for AD.
AD = 20 / (0.5 2
sin 40) – 5 = 26.11 meters
Example – 19
Find the area of the following trapezium.
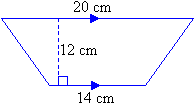
Solution
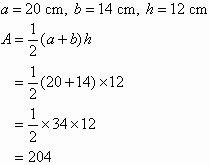
So, the area of the trapezium is 204 m2.
Example – 20
Find the area of the following trapezium.
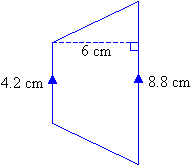
Solution
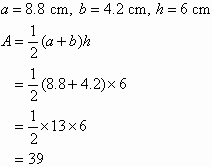
So, the area of the trapezium is 39 cm2.
