Simple Interest-JA
Simple Interest
Interest :
Interest is the time value of money. We may say this is the cost of using capital.
Principal :
It is the borrowed amount.
Amount :
Sum total of interest and principal.
Rate :
It is the rate percentage payable on the amount borrowed.
Period :
It is the time for which the principal is borrowed.
Simple Interest :
Simple interest is payable on principal.
= (P×R×T)/100=where P is the Principal, R is the interest rate, T, is the time.
Amount Due at the end of the time period, A = P (original amount) + SI
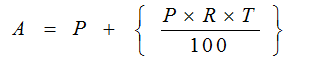
If you have a close look, Simple Interest is nothing else but an application of the concept of percentages.
Question 1:
A certain sum of money amounts to Rs.2000 in 2 years and to Rs.2500 in 3 years. Find the sum and rate of interest.
Solution:
Let P be the amount invested.
Then the amount becomes 2000 in 2 years and 2500 in 3 years. We can see that the amount increases by Rs. 500 between 2nd and 3rd years.
Therefore, we can easily say that the simple interest for 1 year = 2500 – 2000 = 500
So, simple interest for 2 years = 500 x 2 = 1000
From the question, you know that the amount A after 2 years = 2000
Now using the formula A = P + SI,
We can write P = A – SI = 2000 – 1000 = 1000
Now, we know P = Rs.1000, N = 2 years and Simple interest SI = Rs.1000.
If we substitute above values in the formula SI = P*N*R / 100, you will get R as shown below:
R = (100 x 1000) / (1000 x 2)
R = 50%
Therefore, the sum invested P = 1000 and rate of interest R = 50%.
Question 2:
A man borrowed Rs 15000/- at the rate of 24% SI and to clear the debt after 6 years, much he has to return:
Using the Basic Formula: Simple Interest (SI) = (P x R x T)/100
P – Principal amount, T- Number of years, R – Rate of Interest
Given P = 15000, T = 6 Years, R = 24%
Simple Interest (S.I.) = (15000X24X6)/100= Rs 21600
Therefore, total interest = 21600
Total repayment = S.I + Principal amount = 21600 + 15000 = Rs 36600
Question 3:
A man borrowed Rs.12000 at the rate of 10% SI, and lent the same sum to another person at the rate of 15% what will be the gain after 5 years?
Using the Basic Formula: Simple Interest (S.I.) = (P x R x T)/100
P – Principal amount, T- Number of years, R – Rate of Interest
The man borrowed at 10% and he lent the same sum to another person at 15%
Therefore, his gain is actually equal to the different in the interest rate (per year)
= 15 – 10 =5% for 1 year
Thus, to calculate his gain, we use this difference as the rate of interest.
Given T = 5 years and P = Rs. 12000
Amount Gained = (12000x5x5)/100 = Rs 3000
Therefore, his gain = Rs 3000/-
Question 4:
A certain sum of money amounts to Rs. 1008 in 2 years and to Rs. 1164 in 31⁄2 years. find the sum and the rate of interest?
S.I. for 11⁄2years = Rs. (1164-1008) =156
S.I. for 2 years = Rs. (156 x 2⁄3 x 2) = Rs. 208
Principal = Rs. (1008 – 208) = Rs. 800
Now, P = 800, T = 2, and S.I. = 208
Rate = (100×208⁄800×2)% = 13%
Question 5:
At what rate percent per annum will a sum of money double in 8 years.
Let principal = P, Then, S.I.= P and Time = 8 years
We know that S.I. = PTR/100
Rate= [(100 x P)/ (P x 8)]% = 12.5% per annum.
Question 6:
What annual installment will discharge a debt of Rs 1092 due in 3 years at 12% simple interest?
Let each instalment be Rs.x .
1st year = [x + (x * 12 * 2)/100]
2nd year = [ x + (x *12 * 1)/100]
3rd year = x
Then, [x + (x * 12 * 2)/100] + [ x + (x *12 * 1)/100] + x =1092
3x + ( 24x/100 ) + ( 12x/100 ) = 1092
336x =109200
Therefore, x = 325
Each installment = Rs. 325
Question 7:
A sum was put at simple interest at a certain rate for 3 years. Had it been put at 2% higher rate, it would have fetched Rs 360 more. Find the sum.
Let sum = P and original rate = R. Then
[(P * (R+2) * 3)/100] – [ (P * R * 3)/100] = 360
3P*(R+2) – 3PR = 36000
3PR + 6P – 3PR = 36000
6P = 36000
P = 6000
