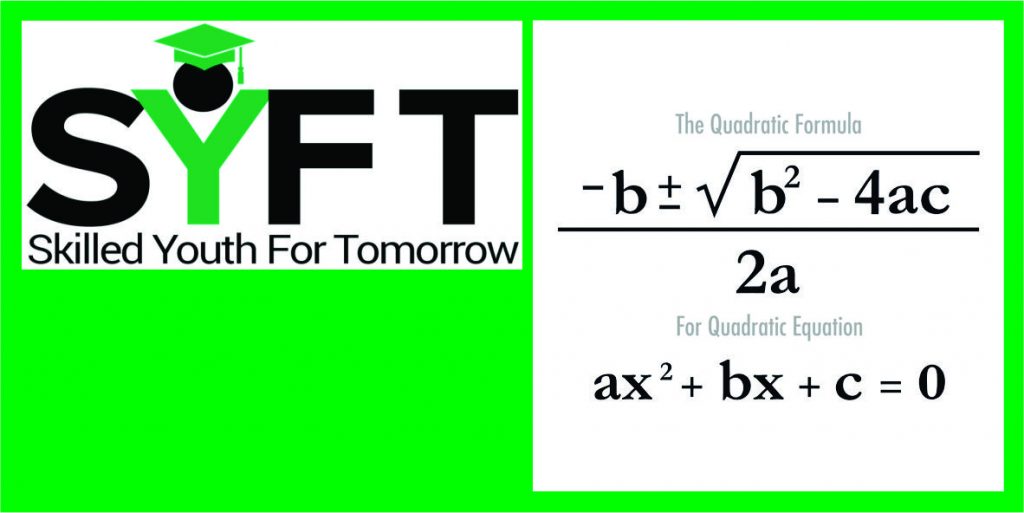What is Quadratic Equation & how it is helpful for us?
An equation where the highest exponent of the variable (usually “x”) is a square (2). So it will have something like x2, but not x3 etc. A Quadratic Equation is usually written ax2 + bx + c = 0. Example: 2x2 + 5x − 3 = 0. The name Quadratic comes from “quad” Meaning Square, because the variable gets squared (like x2). It is also called an “Equation of Degree 2” (because of the “2” on the x). The quadratic formula, is used in algebra to solve quadratic equations (polynomial equations of the second degree). The general form of a quadratic equation is, where x represents a variable, and a, b, and c are constants, with. A quadratic equation has two solutions, called roots. The quadratic function is important, because parabolas predict physics in real life as well as patterns on graphs to help predict the future or future patterns. Help to predict trajectory of an object. This is very useful for real world situations. The main purpose of the quadratic formula is to solve the quadratic equation (sometimes called finding a zero of the equation). That is find x such that f(x) = 0, where f(x) is a quadratic function (a polynomial of degree two). While factoring may not always be successful, the Quadratic Formula can always find the solution. The Quadratic Formula uses the “a”, “b”, and “c” from “ax2 + bx + c”, where “a”, “b”, and “c” are just numbers; they are the “numerical coefficients” of the quadratic equation they’ve given you to solve. In elementary algebra, the quadratic formula is the solution of the quadratic equation. There are other ways to solve the quadratic equation instead of using the quadratic formula, such as factoring, completing the square, or graphing. Using the quadratic formula is often the most convenient way.
Solution of the quadratic equation ax2 + bx + c = o ………………………….(1)
The roots can be found by completing the square in left hand side, As a is not zero
Solving for then gives