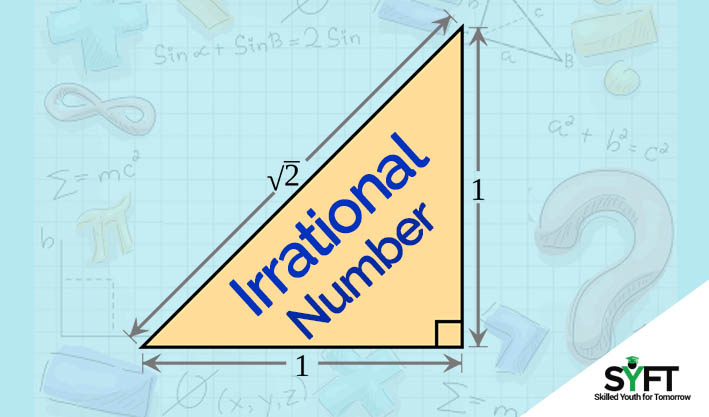
Prove that \sqrt{2} is irrational.
Solution: If not, let us assume \sqrt{2} is rational.
Then \sqrt{2} =p/q (q ≠0 , (p,q) ≠ 2)
=> 2 = p2/q2
=> 2 q2= p2
Now 2 q2 is divisible by 2, hence p2 is divisible by 2
Then p is divisible by 2. Now let p = 2r
2q2 = 4 r2
q2 = 2 r2
q2 is divisible by 2.
q is divisible by 2
It contradicts our assumption that p and q are not divisible by 2.
Prove that is \sqrt{3}irrational.
Solution: If not, let us assume \sqrt{3} is rational.
Then \sqrt{3} =p/q (q ≠0 , (p,q) ≠ 3)
=> 3 =p2/q2
=> 3q2= p2
Now 3q2 is divisible by 3, hence p2 is divisible by 3
Then p is divisible by 3. Now let p=3r
3q2 = 9 r2
q2 = 3 r2
q2 is divisible by 3.
q is divisible by 3
It contradicts our assumption that p and q are not divisible by 3.
Prove that \sqrt{5} is irrational.
Solution: If not, let us assume \sqrt{5} is rational.
Then \sqrt{5} =p/q (q ≠0 , (p,q) ≠ 5)
=>5 =p2/q2
5q2= p2
Now 5 q2 is divisible by 5, hence p2 is divisible by 5
Then p is divisible by 5. Now let p=5r
5q2 = 25 r2
q2 = 5 r2
q2 is divisible by 5.
q is divisible by 5
It contradicts our assumption that p and q are not divisible by 5.