What is Triangle

A triangle is a closed curve which is formed by 3 line segments. The line segments by which the triangle is formed are called sides of the triangle. So, in a triangle, there are 3 sides, 3 vertices and 3 angles.

Here is a triangle name Δ ABC where sides are AB, BA and CA. Vertices are A, B and C. Angles are ∠CAB, ∠CBA and ∠ACB

PARTS OF THE TRIANGLE

There is some terminology associated with the triangles.

Base: Its is the bottom side of the triangle.

Base angles: Two angles which touch the base.

Vertex of the triangle: The angle which is opposite to the base

Legs: The two sides which are not bases.

TYPES OF TRIANGLES

The triangles are classified based on sides and angles.

Based on sides, the triangles are classified as follows.

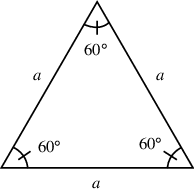
a) Equilateral triangle:

An equilateral triangle in which all three sides (angles) are equal.

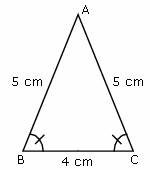
b) Isosceles triangle:

An isosecles triangle in which any two sides (angles) are equal.

c) Scalene triangle:

A triangle in which no two sides (angles) are equal.

Based on the angles the triangles are classified as follows.

a) Acute angled triangle:

Any triangle in which all the angles are less than 90⁰ .

An acute triangle is a triangle with all three angles acute (less than 90°). An obtuse triangle is one with one obtuse angle (greater than 90°) and two acute angles. Since a triangle’s angles must sum to 180°, no triangle can have more than one obtuse angle.

b) Obtuse angled triangle:

Any triangle with one of the angles greater than 90° . An obtuse triangle is one with one obtuse angle (greater than 90°) and two acute angles. Since a triangle’s angles must sum to 180°, no triangle can have more than one obtuse angle.

c) Right angled triangle:

A triangle in which one of the angles is equal to 90° .

A right triangle or right-angled triangle is a triangle in which one angle is a right angle (that is, a 90-degree angle). The relation between the sides and angles of a right triangle is the basis for trigonometry.

Question – 1:

Triangle ABC, shown below, has an area of 15 mm ². Side AC has a length of 6 mm and side AB has a length of 8 mm and angle BAC is obtuse. Find angle BAC to the and find length of side BC.

Solution

Let the size of angle BAC = t. One of the many formulas for the area triangle is.

area = 15 = (1/2) (AC)(AB) sin(t)

Solve for sin(t) to obtain.

sin(t) = 30 / (8*6) = 0.625

solution that gives t obtuse

t = Pi – arcsin(0.625)

Convert t to degrees to obtain

t (approximately) = 141.3 o

We now use the cosine rule to calculate the length of side BC

BC 2 = AB 2 + AC 2 – 2(AB)(AC)cos(t)

= 64 + 36 – 2(8)(6)cos(141.3 o)

BC = 13.23 mm.

Question – 2: 

An isosceles triangle has angle A 30 degrees greater than angle B. Find all angles of the triangle.

Solution :

An isosceles triangle has two angles equal in size. In this problem A is greater than B therefore angles B and C are equal in size. Since angle A is 30 greater than angle B then A = B + 30 o. The sum of all angles in a triangle is equal to 180 o.

(B+30) + B + B = 180

Solve the above equation for B.

B = 50 o

The sizes of the three angles are

A = B + 30 = 80 o

C = B = 50 o

Question – 3: 

Triangle ABC shown below is inscribed inside a square of side 20 cm. Find the area of the triangle

Solution :

The area is given by

area of triangle = (1/2) base * height

= (1/2)(20)(20) = 200 cm 2

Question – 4: 

Find the area of an equilateral triangle that has sides equal to 10 cm.

Solution:

Let A,B and C be the vertices of the equilateral triangle and M the midpoint of segment BC. Since the triangle is equilateral, AMC is a right triangle. Let us find h the height of the triangle using Pythagorean theorem.

h 2 + 5 2 = 10 2

Solve the above equation for h.

h = 5 sqrt(3) cm
We now find the area using the formula.

area = (1/2)* base * height = (1/2)(10)(5 sqrt(3))

= 25 sqrt(3) cm 2 = 43.3 cm 2

Question – 5: 

The right triangle shown below has an area of 25. Find its hypotenuse.

Solution:

Since the x coordinates of points A and B are equal, segment AB is parallel to the y axis. Since BC is perpendicular to AB then BC is parallel to the x axis and therefore y, the y coordinate of point C is equal to 3. We now need to find the x coordinate x of point C using the area as follows

area = 25 = (1/2) d(A,B) * d(B,C)

d(A,B) = 5

d(B,C) = |x – 2|

We now substitute d(A,B) and d(B,C) in the area formula above to obtain.

25 = (1/2) (5) |x – 2|

We solve the above as follows

|x – 2| = 10

x = 12 and x = – 8

We select x = 12 since point C is to the left of point B and therefore its x coordinate is greater than 2.

We have the coordinates of point A and C and we can find the hypotenuse using the distance formula.

hypotenuse = d(A,C) = sqrt[ (12 – 2) 2 + (3 – 8) 2 ]

= sqrt(125) = 5 sqrt(5)