Circular Measure of Angles.

Circular Measure of Angle

Angles can be either straight, right, acute or obtuse. An angle is a fraction of a circle where the whole circle is 360°. A straight angle is the same as half the circle and is 180° whereas a right angle is a quarter of a circle and is 90°.

Radians Measure
To measure angle we have : (i) Degree measure (ii) Radian measure
If an arc of a circle is drawn such that it is the same length as the radius, then the angle created is called one radian as shown in Fig.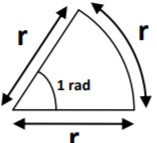
From the diagram you can see that dividing the circumference by the radius will give the number of radians in one complete revolution. Therefore, the number of radians in one revolution is circumference/radius= 2πr/r = 2π

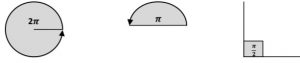
A circle 2π radian             A semi circle π radian           A right angle contain π/2 radian

From the above we can derive the formulas of transforming degrees to radians, vice versa, by using direct proportion as shown below :

An arc of a circle with the same length as the radius of that circle subtends an angle of 1 radian. The circumference subtends an angle of 2π radians. The radian (SI symbol rad) is the SI unit for measuring angles, and is the standard unit of angular measure used in many areas of mathematics.

If arc length = l, then l =r × θ , r is the radius and θ is the angle.

Area of a Sector of a Circle.

Area of a Sector of a Circle = 1/2 × l × r = 1/2 r × θ× r = 1/2 × θ× r²