Linear Equation With Two variables

A linear system of two equations with two variables is any system that can be written in the form.

ax + by = p

cx + dy = q

where any of the constants can be zero with the exception that each equation must have at least one variable in it.

Also, the system is called linear if the variables are only to the first power, are only in the numerator and there are no products of variables in any of the equations.

3x – y = 7

2x + 3y = 1

Before we discuss how to solve systems we should first talk about just what a solution to a system of equations is.  A solution to a system of equations is a value of x and a value of y that, when substituted into the equations, satisfies both equations at the same time.

For the example above  x = 2 and  y = -1  is a solution to the system.  This is easy enough to check.

Here is an example of a system with numbers.

example above  and  is a solution to the system.  This is easy enough to check.

3(2) – (-1)= 7

2(2)+3(-1)= 1

So, sure enough that pair of numbers is a solution to the system.  Do not worry about how we got these values.  This will be the very first system that we solve when we get into examples.

Note that it is important that the pair of numbers satisfy both equations.  For instance  x = 1 and y = -4 will satisfy the first equation, but not the second and so isn’t a solution to the system.  Likewise, x = -1 and y = 1  will satisfy the second equation but not the first and so can’t be a solution to the system.

Now, just what does a solution to a system of two equations represent?  Well if you think about it both of the equations in the system are lines.  So, let’s graph them and see what we get.

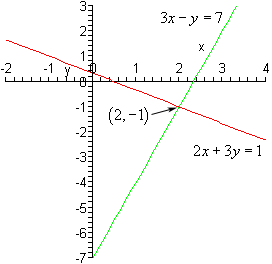
As you can see the solution to the system is the coordinates of the point where the two lines intersect.  So, when solving linear systems with two variables we are really asking where the two lines will intersect.

We will be looking at two methods for solving systems in this section.

The first method is called the method of substitution.  In this method we will solve one of the equations for one of the variables and substitute this into the other equation.  This will yield one equation with one variable that we can solve.  Once this is solved we substitute this value back into one of the equations to find the value of the remaining variable.

In words this method is not always very clear.  Let’s work a couple of examples to see how this method works.

Example 1:  Solve each of the following systems.

3x – y = 7

2x+ 3y = 1

Solution: 

So, this was the first system that we looked at above.  We already know the solution, but this will give us a chance to verify the values that we wrote down for the solution.

Now, the method says that we need to solve one of the equations for one of the variables.  Which equation we choose and which variable that we choose is up to you, but it’s usually best to pick an equation and variable that will be easy to deal with.  This means we should try to avoid fractions if at all possible.

In this case it looks like it will be really easy to solve the first equation for y so let’s do that.

3x- 7 = y

Now, substitute this into the second equation.

2x + 3(3x- 7) = 1

This is an equation in x that we can solve so let’s do that.

 2x + 9x -21 =1

11x = 22

x = 2

So, there is the x portion of the solution.

Finally, do NOT forget to go back and find the y portion of the solution.  This is one of the more common mistakes students make in solving systems.  To so this we can either plug the x value into one of the original equations and solve for y or we can just plug it into our substitution that we found in the first step.  That will be easier so let’s do that.

y = 3x -7 = 3(2)-7 = -1

So, the solution is x = 2  and  y = -1  as we noted above.

Problem 2: The equation 2x + y + 4