Unit Digit-RRB
Unit Digit
For the concept of identifying the unit digit, we have to first familiarize with the concept of cyclicity. Cyclicity of any number is about the last digit and how they appear in a certain defined manner. Let’s take an example to clear this thing:
The cyclicity chart of 2 is:
21 =2
22 =4
23 =8
24=16
25=32
Have a close look at the above. You would see that as 2 is multiplied every-time with its own self, the last digit changes. On the 4th multiplication, 25 has the same unit digit as 21. This shows us the cyclicity of 2 is 4, that is after every fourth multiplication, the unit digit will be two.
Cyclicity table:
The cyclicity table for numbers is given as below:
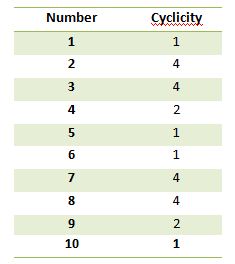
How did we figure out the above? Multiply and see for yourself. It’s good practice.
Now let us use the concept of cyclicity to calculate the Unit digit of a number.
What is the unit digit of the expression 4993?
we have two methods to solve this but we choose the best way to solve it i.e. through cyclicity
We know the cyclicity of 4 is 2
Have a look:
41 =4
42 =16
43 =64
44 =256
From above it is clear that the cyclicity of 4 is 2. Now with the cyclicity number i.e. with 2 divide the given power i.e. 993 by 2 what will be the remainder the remainder will be 1 so the answer when 4 raised to the power one is 4.So the unit digit in this case is 4.
For checking whether you have learned the topic, think of any number like this, calculate its unit digit and then check it with the help of a calculator.
Note : If the remainder becomes zero in any case then the unit digit will be the last digit of acyclicity number
where a is the given number and cyclicity number is shown in above figure.
Example 1: The digit in the unit place of the number 7295 X 3158 is
A. 7
B. 2
C. 6
D. 4
Solution:
The Cyclicity table for 7 is as follows:
71 =7
72 =49
73 = 343
74 = 2401
Let’s divide 295 by 4 and the remainder is 3.
Thus, the last digit of 7295 is equal to the last digit of 73 i.e. 3.
The Cyclicity table for 3 is as follows:
31 =3
32 =9
33 = 27
34 = 81
35 = 243
Let’s divide 158 by 4, the remainder is 2. Hence the last digit will be 9.
Therefore, unit’s digit of (7925 X 3158) is unit’s digit of product of digit at unit’s place of 7925 and 3158 = 3 * 9 = 27. Hence option 1 is the answer.
Example 2: What is the unit digit in the product (365 x 659 x 771)?
A. 1
B. 2
C. 4
D. 6
Solution:
Unit digit in 34 = 1  Unit digit in (34)16 = 1
Unit digit in (34)16 = 1
 Unit digit in 365 = Unit digit in [ (34)16 x 3 ] = (1 x 3) = 3
Unit digit in 365 = Unit digit in [ (34)16 x 3 ] = (1 x 3) = 3
Unit digit in 659 = 6
Unit digit in 74  Unit digit in (74)17 is 1.
Unit digit in (74)17 is 1.
Unit digit in 771 = Unit digit in [(74)17 x 73] = (1 x 3) = 3
 Required digit = Unit digit in (3 x 6 x 3) = 4.
Required digit = Unit digit in (3 x 6 x 3) = 4.
Example 3: 7589 – ? = 3434
A. 4242
B. 4155
C. 1123
D. 11023
E. None of these
Solution:
Let 7589 -x = 3434
Then, x = 7589 – 3434 = 4155
Example 4: The unit digit in the product (784 x 618 x 917 x 463) is:
A. 2
B. 3
C. 4
D. 5
Solution:
Unit digit in the given product = Unit digit in (4 x 8 x 7 x 3) = (672) = 2
Example 5: 3897 x 999 = ?
A. 3883203
B. 3893103
C. 3639403
D. 3791203
E. None of these
Solution:
3897 x 999 = 3897 x (1000 – 1)
= 3897 x 1000 – 3897 x 1
= 3897000 – 3897
= 3893103.
